Bisection Method Program in C and C++

Bisection method is a method used to find the root of a function present between two given values of x. The main idea behind bisection is that the function needs to be continuous. First, two values of x (x1 and x2) have to be provided such that the root of the function lies in the interval of these values. If the provided values do not follow this condition then this method will not work. To check if these values are valid, the value of the function at both of these values of x is calculated and their product should be less than 0. This test indicates that the function is changing sign in this interval. This proves that the function is continuous and there lies a root in this interval.  After this, the midpoint of this interval is calculated (x1+x2/2) and the value of the function at this midpoint is checked. If this value is greater than 0 then a new interval is created by putting the value of x2 equal to the midpoint. Else if the value at midpoint is less than 0 then the value of x1 is put equal to the midpoint and a new interval is created. This is done so that the function still changes sign in the new interval. This is done repeatedly to get a more accurate value of the root of the equation.

Bisection Method Program in C

#include <stdio.h>
#include <conio.h>
#include <math.h>
#define TRUE 1
#define f(x) x * x - 3

void bisectionMethod(double x1, double x2, double y1, double y2, double err){
    double mid, ymid;
    int step = 1;
    printf("\nStep\tx1\t\tx2\t\tmid\t\tf(mid)\n");
    do {
        mid = (x1 + x2) / 2;
        ymid = f(mid);
        printf("%d\t%0.6lf\t%0.6lf\t%0.6lf\t%0.6lf\n", step, x1, x2, mid, ymid);
        if ((ymid * y2) < 0){
            x1 = mid;
            y1 = ymid;
        }
        else{
            x2 = mid;
            y2 = ymid;
        }
        step++;
    } while(fabs(ymid) > err);
    printf("\nRoot of the equation is %lf\n", mid);
}

int main(){
    double x1, x2, y1, y2, err;
    while (TRUE){
        printf("Enter two initial values of x between which the root lies ");
        printf("(First lesser and then the greater value): ");
        scanf("%lf", &x1);
        scanf("%lf", &x2);
        y1 = f(x1);
        y2 = f(x2);
        if ((y1 * y2) >= 0){
            printf("Root does not lie between %lf and %lf\n", x1, x2);
            printf("Try Again!\n");
        }
        else if (x1 > x2){
            printf("Please enter the lesser value first and then the greater value\n");
        }
        else
            break;
    }
    printf("Enter tolerable error: ");
    scanf("%lf", &err);
    bisectionMethod(x1, x2, y1, y2, err);
}

Bisection Method Program in C ++

#include <iostream>
#include <iomanip>
#include <math.h>
#define f(x) x * x - 3

using namespace std;

void bisectionMethod(double x1, double x2, double y1, double y2, double err){
    double mid, ymid;
    int step = 1;
    cout << "\nStep\tx1\t\tx2\t\tmid\t\tf(mid)" << endl;
    do {
        mid = (x1 + x2) / 2;
        ymid = f(mid);
        cout << setprecision(6) << fixed;
        cout << step << "\t" << x1 << "\t" << x2 << "\t" << mid << "\t" << ymid << endl;
        if ((ymid * y2) < 0){
            x1 = mid;
            y1 = ymid;
        }
        else{
            x2 = mid;
            y2 = ymid;
        }
        step++;
    } while(abs(ymid) > err);
    cout << "\nRoot of the equation is " << mid << endl;
}

int main(){
    double x1, x2, y1, y2;
    while (true){
        cout << "Enter two initial values of x between which the root   lies ";
        cout << "(First lesser and then the greater value): ";
        cin >> x1 >> x2;
        y1 = f(x1);
        y2 = f(x2);
        if ((y1 * y2) >= 0){
            cout << "Root does not lie between " << x1 << " and " << x2                       << endl;
            cout << "Try Again!" << endl;
        }
        else if (x1 > x2){
            cout << "Please enter the lesser value first and then the greater value" << endl;
        }
        else
            break;
    }
    double err;
    cout << "Enter tolerable error: ";
    cin >> err;
    bisectionMethod(x1, x2, y1, y2, err);
}

 

Output of Bisection Method Program in C and C++

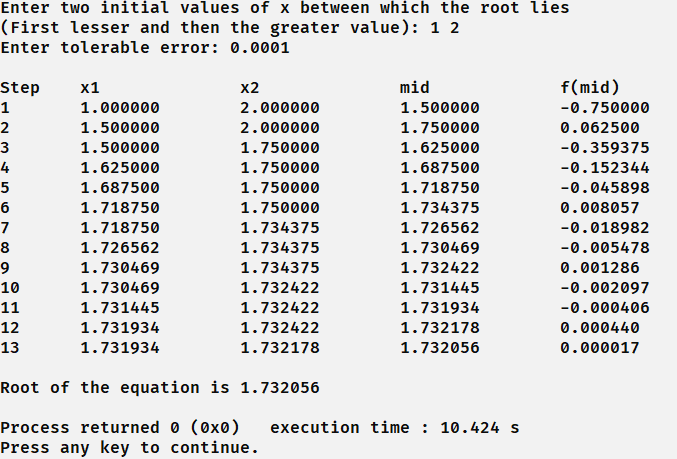
In the above program, the function used is If you want to use your own function then just replace #define f(x) x * x – 3 with #define f(x) your_own_equation. The main () function is used to enter the values of x1 and x2, the interval in which the root lies. To validate these values, a check is also performed. Another value is inputted from the user called maximum tolerable error which is will be used to denote the number of decimals up to which the final answer should be accurate. The bisectionMethod () function is used to print all the operations at every step using do while loop and then to find the final answer accurate up to the tolerable error the user inputted.